Computer Science Enthusiasts in SIS-SMU

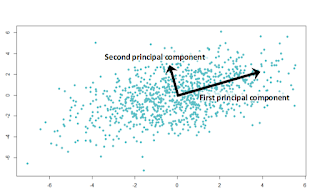
1. What is feature scaling?  Feature scaling is a method used to normalize all independent values of our data. We also call it as data normalization and is generally performed before running machine learning algorithms. 2. Why do we need to use feature scaling?  In practice the range of raw data is very wide and hence the object functions will not work properly (means that it will stuck at local optimum), or they are time-consuming without normalization. For example:  K-Means, might give you totally different solutions depending on the preprocessing methods that you used. This is because an affine transformation implies a change in the metric space: the Euclidean distance between two samples will be different after that transformation. When we apply gradient descent, feature scaling also helps it to converge much faster that without normalized data.  With and without feature scaling in gradient descent 3. Methods in feature scaling? Rescaling The simp...

Topic #1. Distributions of functions of random variables Given random variables drawn from some known distribution, and a function of these random variables. We are interested in finding the distribution of this function's value. We are going through three techniques to find the probability distributions of random variables: distribution function technique, change of variable technique and moment-generating function technique. First, we consider function of one random variable with two techniques: distribution function technique and change of variables technique. Then, we extend the same technique to transformation of two random variables. Next, we consider cases where the random variables are independent, and sometimes identically distributed. After that, we spend sometimes with the third technique, moment generating function, to find the distribution of functions of random variables. - Source      1) https://onlinecourses.science.psu.edu/stat414/node/127

I. What is manifold learning Dimensionality Reduction The accuracy of the training algorithms is directly proportional to the amount of data we have. However, managing a large number of features is usually a burden to our algorithm.  Some of these features may be irrelevant, so it's important to make sure that the final model doesn't get affected by this.  What is Dimensionality?  Dimensionality refers to the minimum number of coordinates needed to specify any point within a space or an object. Why do we need Dimensionality Reduction? If you keep the dimensionality high, it will be nice and unique but it may not be easy to analyse because of complexity involved. Apart from simplifying data, visualization is also an interesting and challenging application. Linear Dimensionality Reduction Fig 1 : PCA illustration (source: http://evelinag.com/blog ) Principle Component Analysis  Given a data set, PCA finds the directions along which the d...